本文共 4109 字,大约阅读时间需要 13 分钟。
文章目录
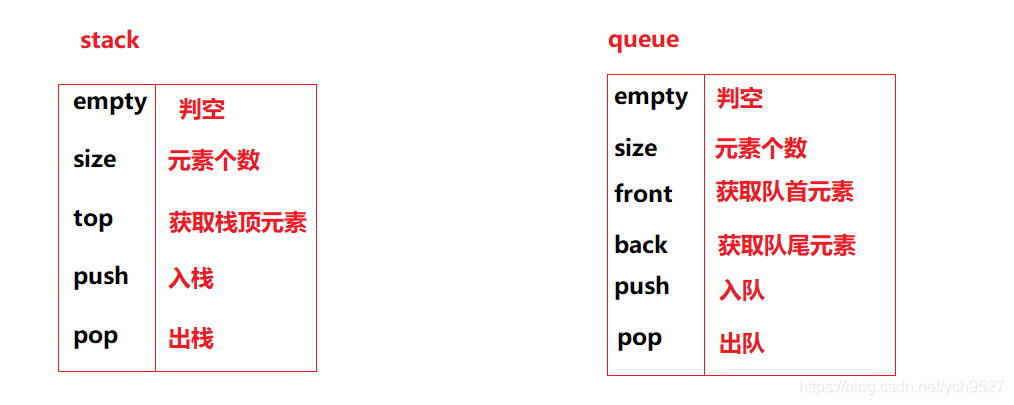
1.栈和队列常用接口
2.容器适配器
容器适配器是一种设计模式(设计模式是一套被反复使用,被广泛认可,经过分类编目的代码设计经验总和),该种模式是将一个类的结构转换成客户希望的另外一个接口
stack和queue,就是容器适配器,因为stack和queue只是对其它容器的接口进行了包装,STL中stack和queue默认使用的是deque
3.deque
双端队列的设计本意是想取代vector和list,最后设计出来的作用没有达到预期,可以说是一种失败的设计
有一句笑点是,用deque来排序,不如将deque里面的数据拷贝至vector中排好序再放回deque之中,这足矣可见deque随机访问的效率是多么的低下了
3.1是什么
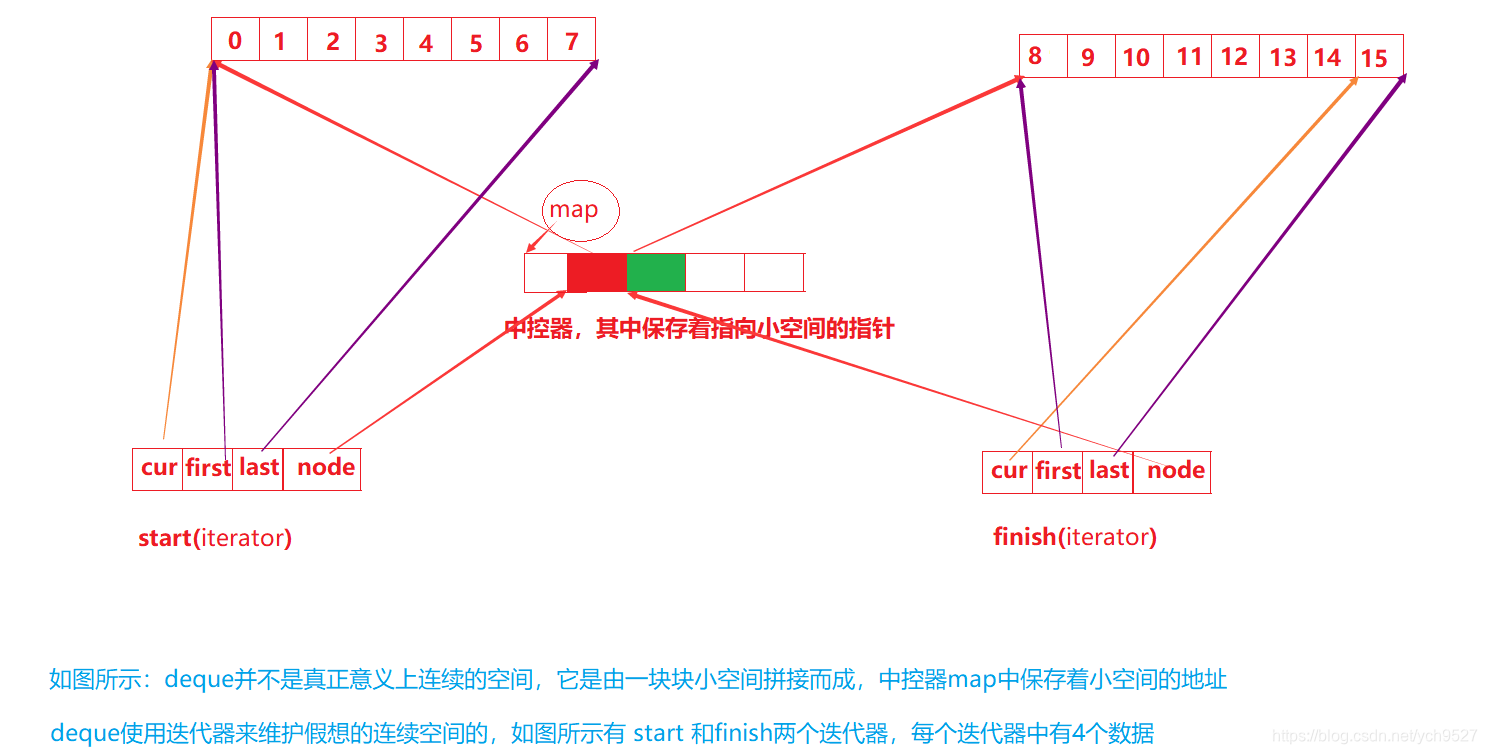
双端队列是一种双开口的“连续”空间的数据结构,它对头尾两端操作的时间复杂度为O(1),它不是队列,而是像vector和list的融合体
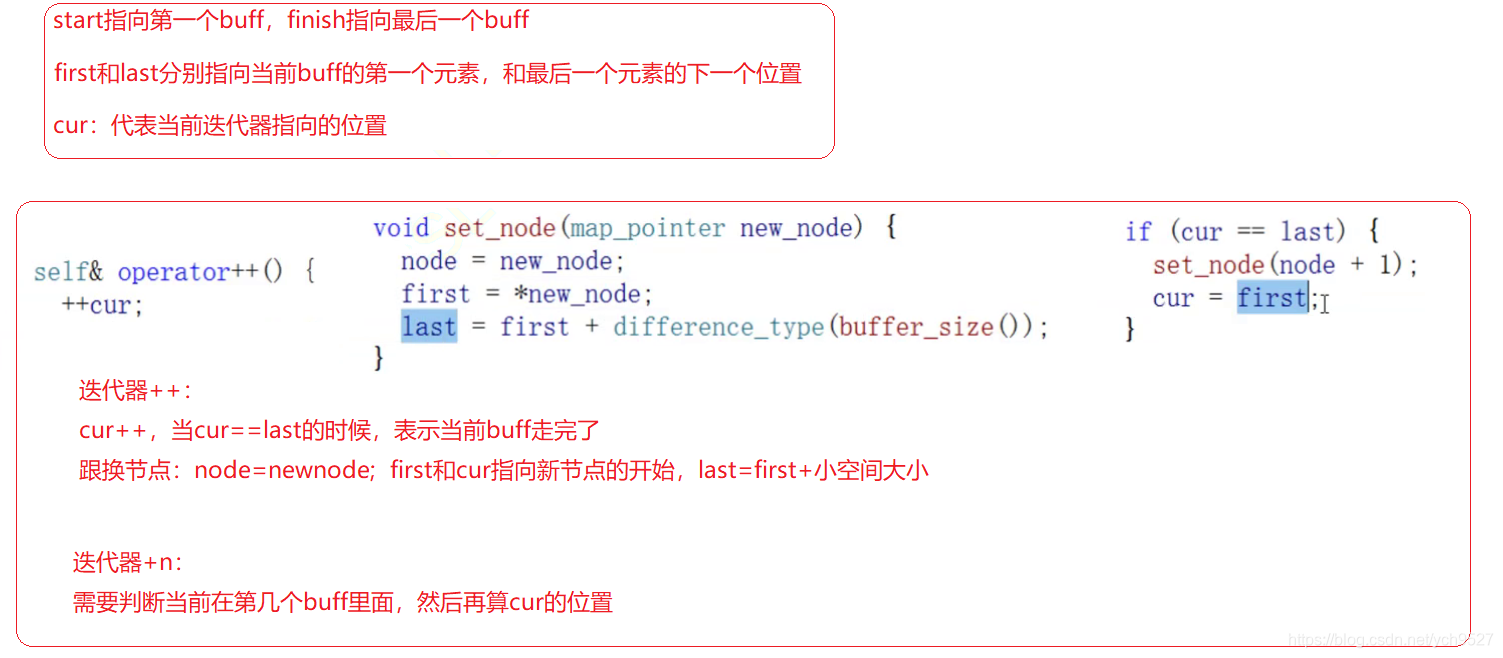
与vector相比,头端操作不需要移动元素 与list相比,缓存命中率高但是,deque并不是真正连续的空间结构,而是由一小段一小段连续的空间拼接而成,deque有点像动态增长的二维数组

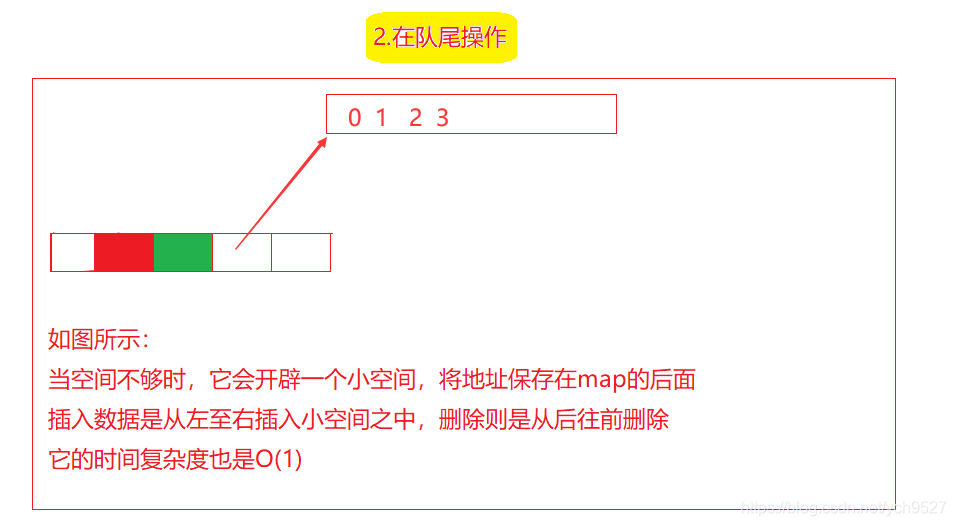

3.2deque的优缺点
优点:
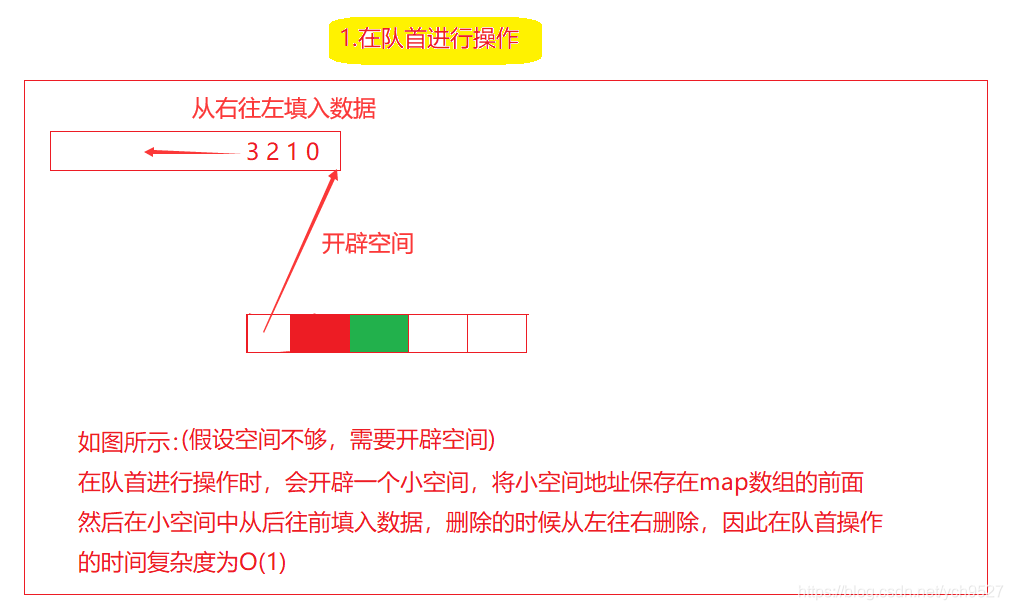
与vector相比,deque在头部的插入和删除,时间复杂度都是O(1)。扩容时也不必搬移大量的数据,效率要高出vector与list相比,deque里面有许多连续的空间,因此缓存命中率要高即空间命中率高,不需要存储额外字段
缺点:
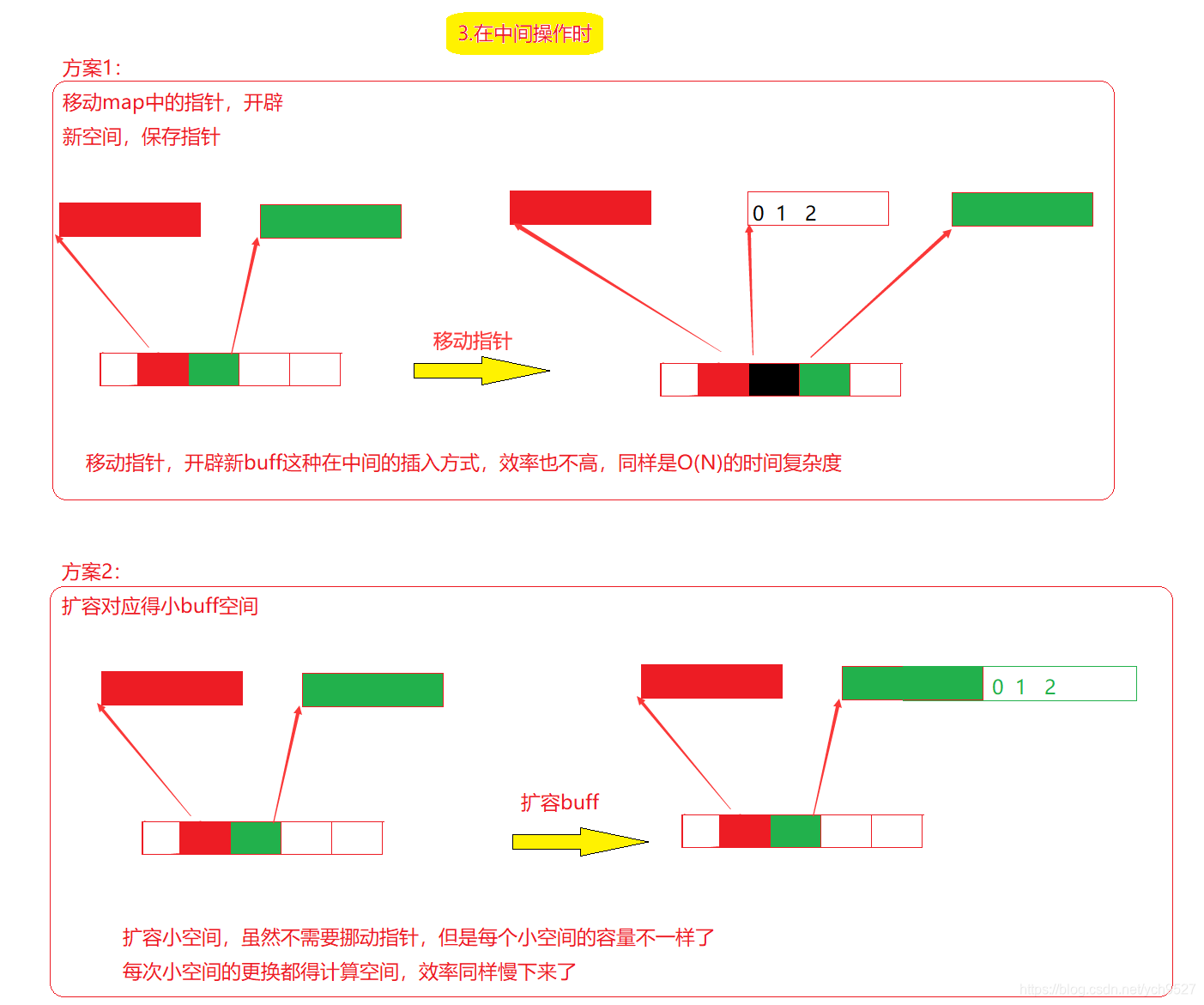
由于deque是由许多小空间构成的,因此下标访问需要大量的计算,判断边界,这样在排序这种需要大量下标访问的操作时,就会导致效率低下。因此deque的实际使用并不多,目前deque都是在STL中用作stack和queue的底层数据结构3.3deque作为stack和queue底层数据结构的优势
1.栈和队列没有迭代器,不需要进行下标访问,并且只在端口处进行操作,而deque的端口处操作时间复杂度为O(1),因此非常适合
2.stack元素增加时,如果使用vector扩容的时候,需要进行数据拷贝,而使用deque扩容的时候不需要进行数据的搬移,效率比vector高
3.queue元素增加时,deque不仅仅效率高,内存使用率要也要高于list
3.4总结
要想设计出一个数据结构既包含vector的优点,又包含list的优点,这种设计就是deque,但是它失败了
因为C++ 是一门比较关注效率的语言,因此实际是上没有这种完美的数据结构4.stack模拟实现
template> class stack { public: stack() { } bool empty() { return _con.empty(); } size_t size()const { return _con.size(); } const T& top() { return _con.back(); } void push(const T& x) { _con.push_back(x); } void pop() { _con.pop_back(); } private: Container _con; };
5.queue模拟实现
template> class queue { public: queue() { } bool empty() { return _con.empty(); } size_t size()const { return _con.size(); } const T& front() { return _con.front(); } const T& back() { return _con._back(); } void push(const T& x) { _con.push_back(x); } void pop() { _con.pop_front(); } private: Container _con; };
6.仿函数
仿函数就是一个类,只不过是重载了 operator (),而这个类的对象可以像函数一样去用,因此叫做仿函数
一些情况下,需要进行大于或者小于的比较,比如我们的排序,按照正常情况,大于小于需要写两遍几乎一样的代码,只是比较部分不一样,这样导致代码很臃肿。
而利用仿函数,重载()操作符,实现大小的比较,即可以通过更换传入的仿函数,来使模板参数的推演类型发生变化,进而使代码产生不同的效果6.1仿函数的应用场景一:实现大小堆
对一个堆进行常规操作,这个堆中一定要有向上调整和向下调整两个算法,然后普通的实现方法,一次代码只能实现一种堆,因为一次只能进行一次">“或者”<"的比较。
这时候如果在类的模板参数中,添加一个仿函数模板参数,通过改变传入的仿函数,即可以实现大小堆的自由切换

6.2仿函数应用场景二:实现商品排序
比如们买的东西的时候,需要按不同的类型进行排序,如果按照常规的代码编写只能按照一种方式进行排序,这时候仿函数的作用就体现出来了



7.优先级队列
7.1优先级队列是什么
优先级队列入数据没有要求,出数据出优先级高的(默认是大堆)
优先级队列被实现为容器适配器,默认使用vector(不满意可以自己传参)作为底层存储数据的容器,在vector上又使用了堆算法将vector中元素构成堆的结构需要注意的是:传入less是大堆,传入greater是小堆,是相反的
7.3优先级队列的模拟实现
优先级队列底层使用的容器应该满足以下几个接口条件:
1.empty() 2.size() 3.front() 4.push_back() 5.pop_back() 6.支持随机访问[]#pragma once#includeusing namespace std;#include #include #include #include template class Greater//仿函数{ public: bool operator ()(const T &x, const T &y) { return x > y; }};template class Less//仿函数{ public: bool operator ()(const T &x, const T &y) { return x < y; }};namespace my{ template ,class Compare=Greater > class priority_queue { public: void ShiftDown(size_t parent) { Compare com; size_t child = parent * 2 + 1; while (child < _con.size()) { if (child + 1 < _con.size() && com(_con[child+1] , _con[child])) child++; if (com(_con[child] ,_con[parent])) swap(_con[child], _con[parent]); else break; parent = child; child = 2 * parent + 1; } } void ShiftUp(size_t child) { Compare com;//仿函数 size_t parent = (child - 1) / 2; while (child > 0)//有孩子一定有父亲 { if (com(_con[child] , _con[parent])) swap(_con[child], _con[parent]); else break; child = parent; parent = (child - 1) / 2; } } priority_queue() = default;//和priority_queue()等价,都是强制编译器生成一个默认的构造函数,用来初始化成员 template priority_queue(InputIterator first, InputIterator last) :_con(first, last)//在这里传迭代器进行初始化 { /*for (int i = (_con.size() - 2) / 2; i >= 0; i--)//向下调整建堆 { ShiftDown(i); }*/ for (size_t i = 1; i <_con.size(); i++) { ShiftUp(i);//向上调整建堆 } } bool empty()const { return _con.empty(); } const size_t size()const { return _con.size(); } const T& top()const { return _con.front(); } void push(const T &x) { _con.push_back(x); ShiftUp(_con.size()-1);//向上调整 } void pop() { assert(!_con.empty()); swap(_con[0], _con[_con.size() - 1]); _con.pop_back(); ShiftDown(0);//向下调整 } private: Container _con; };}
转载地址:http://ghse.baihongyu.com/